인공지능을 설게하는 데 있어서 가장 중요한 요소 중 하나가 바로 Loss function이다.
- 정의:
Loss function은 신경망의 예측 결과값이 바람직한 출력(ground truth 값)으로부터 얼마나 '동떨어졌는지'를 측정하는 수단이다. loss 값이 클수록 모델의 정확도가 낮다는 뜻이고, loss 값이 작으면 모델의 정확도가 높다는 뜻이다. loss 값이 클수록 정확도를 개선하기 위해 모델을 더 많이 학습시켜야 한다.
- 목적:
Optimization. 오차 계산을 통해 파라미터 값 조정을 통해 모델을 최적화 시키기 위함이다. 즉, loss 값이 최소가 되게 하는 최적의 파라미터(가중치) 찾기!
대표적인 최적화 기법: 배치 경사 하강법, 확률적 경사 하강법, 미니배치 경사 하강법 등
- 특징:
loss 값은 언제나 양수이다.
(신경망으로 예측하려는 2개의 데이터 점이 있을 때, 첫 번째 점에 대한 예측의 오차는 10, 두 번째 점에 대한 예측의 오차는 -10이었다면, 평균 오차는 0이 될 것이다. 오차끼리 상쇄되어서는 안된다.)
(양궁과 같이 생각하면 된다. 표적의 가운데는 10점, 중앙에서 벗어날수록 점수가 낮아진다. 이때, 어떤 방향으로 벗어났는지는 중요하지 않다. 중앙에서 얼마나 떨어져있는지에 주목해야한다.)
- 대표적인 Loss function:
- 평균제곱오차(MSE, Mean Squared Error) : 출력값이 실수인 회기 문제에서 널리 사용하는 loss function이다. 오차값이 항상 양의 값이며, 오찻값이 그대로 결과에 대한 평가가 되므로 계산이 간편해진다. 하지만 예욋값에 대해 민감하다.


- 절데제곱오차(MAE, Mean Absolute Error) : 예욋값으로 인해 모델의 대칭성이 깨지면 안되는 경우, MSE의 변종 중 이런 목적에 적합한 함수이다.

- 교차 엔트로피(cross-entropy): 확률 분포 간의 차이를 측정할 수 있다는 특성 덕분에 주로 분류 문제에서 많이 사용한다.
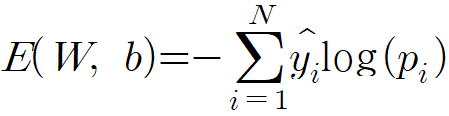
예시를 들자면, 오렌지 이미지 한 장(Image i)을 (사과, 오렌지, 레몬) 세 클래스 중 하나로 분류하려고 한다. 이때, Image i의 실제 확률 분포는
[실제 확률 분포]
P(사과) = 0.0
P(오렌지) = 1.0
P(레몬) = 0.0
이다. 머신러닝 모델 A와 모델 B를 통해 얻은 예측 결과의 확률분포는
[A 모델의 예측 결과 확률 분포]
P(사과) = 0.2
P(오렌지) = 0.3
P(레몬) = 0.5
[B 모델의 예측 결과 확률 분포]
P(사과) = 0.3
P(오렌지) = 0.5
P(레몬) = 0.2
라고 할 때, 교차 엔트로피 식을 이용하여 loss 값을 비교해보면,
E_A = - ( 0.0 * log(0.2) + 1.0 * log(0.3) + 0.0 * log(0.5) ) = 1.2
E_B = - ( 0.0 * log(0.3) + 1.0 * log(0.5) + 0.0 * log(0.2) ) = 0.69
로 B의 loss값이 작아 B가 더 이상적인 모델이라고 판단할 수 있다.
더보기
「비전 시스템을 위한 딥러닝」, 모하메드 엘간디 에서 필요한 내용 일부 발췌 + 내용 정리 하였음.
'AI&ML > 환경구축 & basics' 카테고리의 다른 글
| conda 환경에서 모듈 설치 순서 (0) | 2023.07.28 |
|---|---|
| pytorch cuda 설치 (0) | 2023.04.05 |
| module, library(package), framework, SDK, API 용어 개념 정리 (0) | 2023.02.13 |


